Analyzing Gödel’s Incompleteness Theorem

Throughout history, people have sought to identify accurate statements about the world, so as to better understand the state of our existence. In many domains, this is a difficult endeavor – the world is often messy and inexact, and does not lend itself to easy classification. However, certain simplified domains have yielded more easily; particularly logic and mathematics. Within a given logical or mathematical system, we define the initial rules (known as axioms) from which the system is built up, and by picking the right rules we can ensure regular behavior and an ability to make useful statements. For example, a particular logical system might have the following rules (in addition to axioms allowing for comparisons, evaluation, etc.):

• All bloops are looms
• All looms are toobs

We can make then make statements about the system such as:

1. All bloops are toobs
2. All toobs must be bloops

Based on our rules, statement 1 would evaluate to true and statement 2 to false (note that under different rules their evaluations may differ). Bloops and toobs are both logical entities which exist within the system (based on the initial rules), and so it makes sense that we’re able to say things about them, and evaluate whether those statements are true or false. We can also make more complex statements:

The statement “All bloops are toobs” is false.

Here, we’ve made an observation not about a “first-level” logical entity (i.e. bloops, looms, or toobs), but rather about a logical statement itself (which says something about these first-level entities). To evaluate this statement, we need to first evaluate “All bloobs are toobs” (which is true). Once we’ve done this, we can see that the above sentence is false (because “All bloops are toobs” is true). Though references to other statements complicate the evaluation process, so far they don’t cause any issues – but we still have another type of statement to examine:

This statement is false.

Now our statement no longer says things about bloops and toobs, and instead says something about itself. We can write this statement in another way which drives home the point:

“This statement is false” is false.

How might we interpret this statement? To start, we might try to take it at face value, and assume that the statement “This statement is false” is false. If that’s the case, however, then the statement itself must be true, as it then correctly identifies that it is false! If we try instead to treat the statement as true, we run into the same issue, for now the statement itself must be false (as it says it is false, not true). 

This statement is paradoxical, and clearly cannot be evaluated as either true or false within our logical system. But what drives this paradox? Why is it that we can sometimes make statements about other statements without issue (e.g. “The statement “All bloops are toobs” is false”), but other times run into circularities? The key seems to be self-reference. Because the statement “This statement is false” says something about itself, a possibility opens up for undefined behavior, as the statement must now be evaluated in two different contexts (both at face value, and as a statement about itself). 

While self-reference creates issues, it also seems to be something that is possible only because we’re using the broad domain of natural language to define our statements. Instead, we could imagine using a more limited domain which has been designed to eliminate the possibility for self-reference. This was a goal of mathematicians in the early 20th century, with a notable attempt made by Alfred North Whitehead and Bertrand Russell in their Principia Mathematica. By starting with a handful of initial rules (e.g. “x + 0 = x”, “x * 0 = 0”), they sought to create a system which could prove (or disprove) any statement about natural numbers (a property known as completeness) and which resulted in no contradictions (a property known as consistency). Due to the behavior we observed above, it was critical for them to construct the system in such a way as to avoid self-reference, while also making sure the system was “powerful” enough to say everything there was to say about the natural numbers. 

On first glance, their goal seems to have been a reasonable one. The types of things we want to say about numbers (e.g. that they’re even, square, factorable, prime, etc.) do not seem to require any self-reference. We can start from our initial rules, combine them together in exactly specified ways, and eventually cover the entire domain of statements about natural numbers. One helpful visualization is to think of the initial rules as individual LEGO pieces, and statements about natural numbers as specific combinations of these pieces. For example, there’s a structure that can be built which defines the notion of “prime”, another which says “7 is prime”, and another which says “31 is prime” (but no structure which says “4 is prime”, though “4 is not prime” can be built). 

Although Whitehead and Russell’s goal seems reasonable, Kurt Gödel showed that it was not achievable. His means of doing so was quite creative, and stemmed from his recognition that a particular statement (which you may recognize from above), if constructed in Principia Mathematica, would remove any possibility for the achievement of both completeness and consistency:

This statement is not provable in Principia Mathematica.

This statement is very similar to the one reviewed above, except that “false” has been replaced with “not provable in Principia Mathematica”. This results in a related but slightly different paradox – now, if the statement is indeed not provable, then Principia Mathematica is incomplete (for it cannot prove a valid statement), and if it is actually provable, then Principia Mathematica is inconsistent (for this proof must show the statement is unprovable). 

Although this statement would present issues, on the surface it does not appear to be a statement about natural numbers. In fact, it seems like exactly the kind of statement which Principia Mathematica was explicitly designed to avoid. This is where Gödel’s creativity came in. He realized that each statement of Principia Mathematica could be represented by a particular natural number (using an encoding system of which the details aren’t important – even ASCII could in theory be used with some slight modifications). For example, the statement “2 + 2 = 4” might be represented by the number 4682350000, and the statement “2 + 2 = 5” by 5344390000. More complex statements (e.g. “31 is prime”) require much larger numbers, but size doesn’t matter – the only requirement is that all statements can be represented uniquely. 

Given this encoding, Gödel created a new number category (similar to odd, even, or prime) which we’ll call G-valid. A number is G-valid if the statement it represents (e.g. “2 + 2 = 4” for 4682350000) is provable within Principia Mathematica, and is not G-valid otherwise (e.g. 5344390000, as it represents “2 + 2 = 5”).

It may be apparent already that self-reference is creeping back into the system, with Principia Mathematica saying things about what Principia Mathematica is capable of proving. However, at the statement level, we’re still dealing only with reference (not self-reference), akin to “The statement “All bloops are toobs” is false.” It took another (slightly more complicated) trick by Gödel to recreate the desired statement (“This statement is not provable in Principia Mathematica”). 

Gödel realized that he couldn’t craft the above statement directly, as there was no way for him to say “this statement” (he could only use the Gödel number of a given statement, and the Gödel number of the above statement would necessarily be different than that of any part of it). Instead, he attacked the problem indirectly, using a technique known as diagonalization. Two more functions are required before working through the diagonalization process: a provability function P(x), which, given a particular input value, determines whether or not the statement associated with that input value can be proven in Principia Mathematica (i.e. whether or not the given number is G-valid), and a negation function, Not(x), which returns the opposite of its input.

The first step in the diagonalization process involves laying out (in theory) all possible functions which depend on a single variable (note that this is a slight simplification – in reality, this step only involves all primitive recursive functions, but that distinction isn’t required to get a feel for the process). For example, first you might have F₁(x) = x, then F₂(x) = 2x, then F₃(x) = x², etc. (there’s an infinite number of possible functions, but that’s okay). 

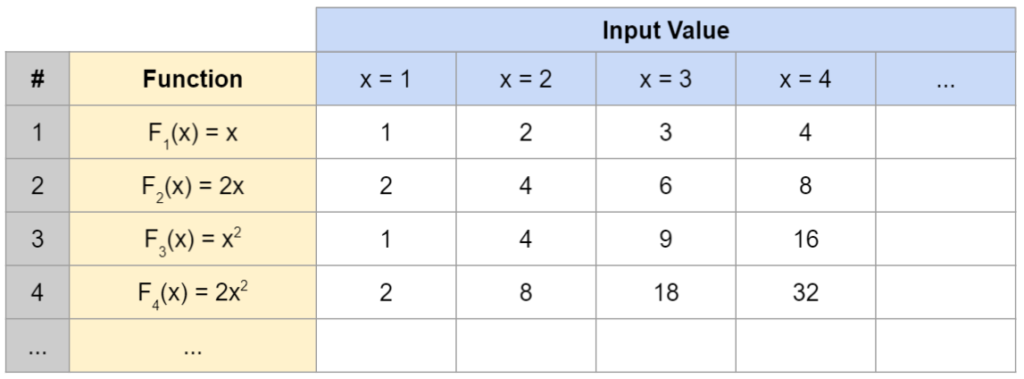
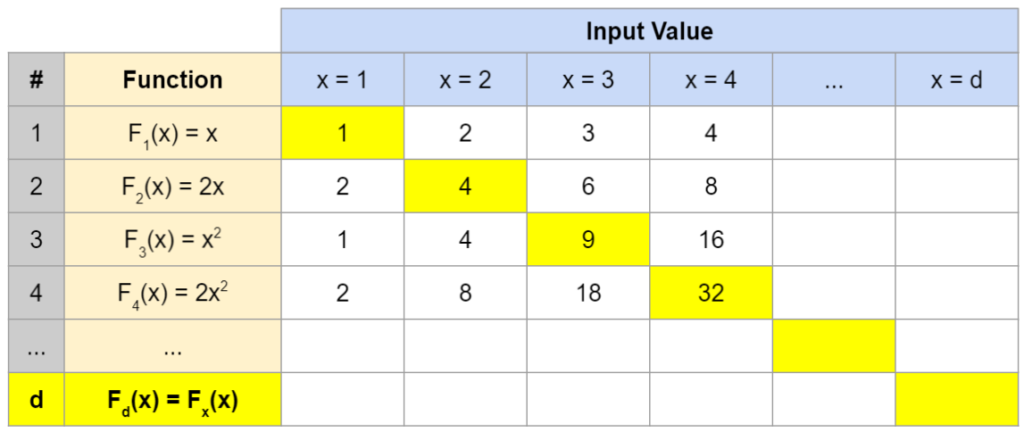
We’ve only listed simple functions here, but as this list covers all possible single variable functions, we can see it must contain some interesting ones (e.g. F(x) = x^{Graham’s Number}, F(x) = x-x+x-x+x-x+x-x). One especially interesting one is the diagonalization function F_d(x) = F_x(x). This function incorporates the whole list of functions we’ve just laid out, and selects which function to use based on the input value (e.g. with an input of 1, it uses F₁(1), giving a value of 1; with an input of 2, it uses F₂(2), giving a value of 4). We can see that the values for this function will equal those on the diagonal of the table we’ve laid out (hence “diagonalization”). 

We can now incorporate our P(x) and Not(x) functions from above with the diagonalization function to generate another interesting function on the list (the most interesting one yet, and the final one required to achieve Gödel’s goal). This new function is F_g(x) = Not(P(F_d(x))), or with substitution, F_g(x) = Not(P(F_x(x))). Essentially, this function returns “no” if F_x(x) is G-valid (as P(F_x(x)) by itself returns “yes”), and “yes” if x is not G-valid. In more regular language, F_g(x) can be viewed as saying:

Statement F_x(x) is not provable in Principia Mathematica.

We’re now quite close to our target statement. F_g(x) says something about the statement F_x(x), but F_x(x) incorporates all possible functions, including F_g(x). All that’s left is to set x equal to g. 

When x = g, our function now says F_g(g) = Not(P(F_g(g))). Again converting to regular language, we can read F_g(g) as saying:

Statement F_g(g) is not provable in Principia Mathematica.

Or alternatively (and more strikingly):

This statement is not provable in Principia Mathematica.

Even in a system explicitly designed to keep out self-reference, Gödel showed that it still manages to show up. It takes some creative steps (e.g. laying out all possible functions) to do so, but nonetheless shows the difficulty of trying to separate “things talked about” (e.g. numbers and their properties) from “the system used to talk about them” (e.g. Principia Mathematica). 

The first time I was introduced to Gödel’s Incompleteness Theorems (in Douglas Hofstadter’s I am a Strange Loop), I didn’t really see the point. It seemed like just a trick, something that arose from wordplay in the domain of natural numbers. The rest of Hofstadter’s book resonated quite strongly with me (and actually started me down the path leading to this blog), but the several chapters devoted to Gödel’s work rang somewhat hollow. Looking back, it seems the point I missed was that the steps Gödel took were, at their core, no different than those steps followed for any other mathematical advancement. Take prime numbers, for example. The first person to analyze prime numbers noticed a particular pattern (i.e. that some numbers are only divisible by 1 and themselves) and then laid out rules to define this behavior and verify whether a particular number was prime. The “primeness” of natural numbers existed before this step was taken; the action of defining merely codified it in the system. Similarly, the G-validity of natural numbers existed before Gödel’s work – just like “primeness”, it is a property of numbers which any complete system would need to prove. The self-reference which occurs is not a “trick”, but rather an outcome of the vastness of the properties of numbers. The interactions between a given number and a given system (e.g. Principia Mathematica) are necessarily among those properties which any complete system would need to prove, and Gödel’s work served to shine a light on this requirement.
With this updated view of the impact of Gödel’s work, its relation to our “I”s (the point Hofstadter was making) becomes more clear. Just as Principia Mathematica seeks to prove (“understand”) all there is to know about natural numbers, our brains (in a broad sense) seek to understand all they can about the natural world. Our brains are pattern-recognizing machines, working to make sense of the world’s regularities. However, just as one thing to know about natural numbers is how Principia Mathematica interacts with them (e.g. what it can and can’t prove), one thing for our brains to know about the world is how our brains interact with it (as we are a part of the world). Beyond this point, the analogy diverges; Principia Mathematica’s interactions with natural numbers are an infinitesimally small portion of all there is to know about numbers, while for our brains, knowledge of how we engage with the world is of the highest importance. Accordingly, our brains form a powerful representation of that engagement – which, from the inside, seems to feel like an “I”.